Безплатни вибрации и колебания системи

В урока бих искал просто да даде на студентите в сравнение колебания през пролетта и математически махала. Имайте предвид сходството на процесите, същата промяна в енергия (кинетична и потенциална) на редовни интервали.

Забележка за формата на обяснение на материали за обучение: на борда по-лесно да намерите снимки махала рамо до рамо, разделен на полупансион. Записванията за описанието на характеристиките на махала правят по едно и също ниво.

1. Въведете понятието колебания системи,
2. Да разгледаме примери за математическо махало и пролетта характеристика на свободните трептения.
3. Определяне на идеалните параметри на колебателните системи.
4. Научих да се направи разграничение на основните характеристики на колебателните системи.
5. Формиране на нови изисквания за знания, предмет асимилация.

1. Pendulum.
2. Пролет махало.

I. организационния точка (2 минути).

II. Проверка на домашното (7 мин.)

Двама студенти в борда решат на задачите (сканиране и фиксиране на домакинствата материал):

1. От известно време махалото ще направи 30 трептения, ако периодът на трептене на 0,5 секунди? Каква е честотата на трептене?
2. Периодът на трептене на крилата Bumblebee 5 мс и комар 600Hz крило на честота на трептене. Кой ще направи повече насекоми размаха крилца в една минута и с колко?

Докато момчетата решават проблемите на черната дъска в клас, проведено челен анкета:

1. Какви са вибрациите?
2. Дайте примери за трептения в природата и технологиите.
3. Какъв е срокът на трептене? Единици за измерване?
4. Каква е честотата на трептене? Единици за измерване?
5. Какво е амплитудата на колебанията?

Ние проверяваме и отписване на предизвикателства от дъската, да коригирате формата и запис разтвор.

III. Пояснение на новия материал (25 мин.)

Демонстрация на осцилаторна обработва памук и пружина махало.

Ако ви донесе на системата от равновесното си положение, може да се отбележи, че след известно време са заглушени вибрациите. Защо колебания са възможни?

При селектирането на системи от равновесното си положение, той се предава количество енергия, така че има колебания. Енергията идва към своя край, системата спира.

Тези колебания срещащи се само заради първоначалното количество енергия, наречени свободни трептения.

След това, тялото е свързана с пружина и печати, суспендира се с резба, наречен осцилаторни системи.

Или физическа система (тялото), в която отклонение от равновесното положение и се издигне колебания наречен осцилаторна система.

Махала: памук и пружината може да се дължи на системата за осцилаторна.

Въпреки това, за да се определят основните характеристики, определени за системите за колебания, ние приемаме, че в рамките на кратък период от време, загуба на енергия в вибрационно движение са достатъчно малки, за да бъдат определени като незначителни. След това системата може да се счита за идеален.

Имайте предвид, че математическата и пролетта махалото - това е идеалният модел на въртящи се системи, в които няма триене. Подобни системи имат, тъй като всяко физическо тяло, притежават механична енергия.

(Бордът е по-удобно да се организира модели махала следващото разделяне борда половини. Сравнение на махалото, на вибрационни характеристики на процеса в сравнение).

Spring махало - вибрираща система, състояща се от маса точка тегло М и пружината, при движение не действа сила на триене.

Период пружина махало трептения могат да бъдат открити с формула

където к - пролет коефициент скованост на махалото. Както следва от формула получен, периода на трептене на махалото пружината е независим от вибрации амплитуда (в право satisfiability Хук).

Енергията на колебанията на пролетта с махало:

- колебания - е размерът на потенциалната енергия на пролетта и кинетична енергия на товара.

Формула потенциални и кинетични енергии:

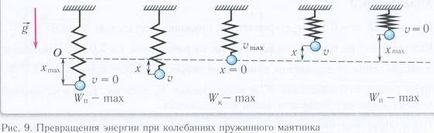
Да разгледаме поведението на махалото и промяната в енергийната си в различни позиции:

1 - (горната позиция) х - преместване макс, о - скорост е 0,

х зависи от потенциалната енергия, следователно E Стах и ​​кинетичната енергия, свързана със скорост V, така E = 0.

Преходът от 1-2 придружава от промени в следните стойности:

X - се намалява, Е намалява о, - повишена E - се увеличава.

2 - (тяло преминава позиция на равновесие)

V - скорост при преминаване равновесното положение е най-големият, о - макс следователно Е - макс.

2-3 преход от позиция се появява с нарастващи х, потенциалната енергия се увеличава и v- скорост намалява и следователно кинетичната енергия също намалява.

3 - (най-вдясно позиция на тялото)

х - преместване макс, о - скорост е 0, така Етах и ​​следователно кинетичната енергия е = 0.

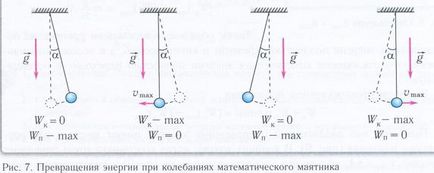
Помислете за един прост махало - една топка окачен на дълъг силна нишка. Такава махало се нарича физически.

Ако размерът на топката е много по-малка от дължината на нишката, а след това тези размери могат да бъдат пренебрегвани. Stretch прежди също могат да бъдат пренебрегнати, тъй като той е много малък. Ако теглото на преждата е много пъти по-малка от масата на топката, теглото на преждата също могат да бъдат пренебрегнати. В този случай,

имаме модел на махалото, която е математически махало.

Математически махалото се нарича материална точка маса m, суспендиран в безтегловност неудължаващ дължина прежда л в гравитационното поле (или други сили)

Период малък математически махало трептене в земната гравитация се определя от Хюйгенс:

Енергията на колебанията на пролетта с махало:

- колебания - е размерът на потенциалната енергия на пролетта и кинетична енергия на товара.

Формула потенциални и кинетични енергии:

IV. Обобщаване материал. (6 мин.)

Тялото може да изпълнява повтарящи се движения около фиксирана точка. Параметрите на промените в трептящи система: положение на тялото. Неговата скорост, кинетичната и потенциална енергия.

Дайте примери за неговото люлеене в движение.

Студентите могат да дадат примери за осцилиращи тела от околните живот.

V. домашното (2 минути).

P. 25, 26 Ex. 23 (1), Пример 24 (2)