Махало период и ускоряване на формула
Окачването е системата, която се състои от материална точка (тяло), който виси на безтегловност неудължаващ нишки (масата й е нищожен в сравнение с теглото на тялото) по еднакъв гравитационно поле, наречен математически махалото (друго име - генератор). Има и други видове устройства. Вместо нишка безтегловност прът може да се използва. Pendulum могат ясно да разкрие същността на много интересни явления. Когато малка амплитуда на вибрациите на неговото движение се нарича хармонични.
Обща информация за механична система

Ако махалото е в състояние на равновесие (окачена вертикално), силата на тежестта ще бъде базирана сила прежда напрежение. Плосък махало на не-разтегливи прежди е система с две степени на свобода на комуникацията. При смяна само на един компонент от което променя характеристиките на всички негови части. Например, ако нишката се заменя с пръчка, то това механична система е само една степен на свобода. Какво тогава свойствата на математическо махало? В тази проста система, под влиянието на периодична смущение, се появява хаос. В този случай, когато точката на спиране не се движи, и се колебае махало има ново равновесно положение. Ако бързи колебания нагоре и надолу, тази механична система става стабилна позиция "с главата надолу". Тя също има своето име. Тя се нарича Капица махалото.
Свойствата на махалото
• Ако, като същевременно се поддържа една и съща дължина на махалото, спряно от различни натоварвания, периодът на трептенията получите същото, въпреки че теглото им ще се различават значително. Следователно периодът на махалото не зависи от теглото на товара.
• Ако системата започва да намалява през махалото не е твърде голям, но под различен ъгъл, тя ще се колебаят с същия период, но на различни амплитуди. Докато отклонения от центъра на баланс не е прекалено големи колебания в тяхната форма ще бъдат достатъчно близо хармоничен. Периодът на такова махало не зависи от вибрационната амплитуда. Това свойство на механичната система се нарича isochronism (на гръцки "Кронос" - време "Izosov" - равен).
Периодът на прост махало
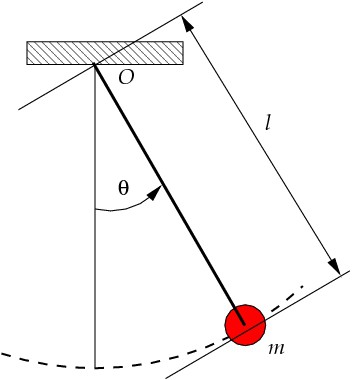
Тази цифра представлява продължителността на периода на трептене. Въпреки комплекс състава, самият процес е много проста. Ако дължината на прежда математическо махало л и гравитационното ускорение д, тази стойност е равна:
Малък период от естествените колебания по никакъв начин не зависи от масата на махалото и амплитудата на колебание. В този случай, като математическа махало се движи с намалена дължина.
Трептенията на математически махало
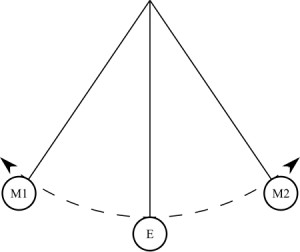
Математически махалото се колебае, който може да бъде описан с обикновено диференциално уравнение:
х + ω2 грях х = 0,
където х (Т) - неизвестна функция (това ъгълът на отклонение от долно положение на равновесие по време Т, изразени в радиани); ω - положителна константа, която се определя от параметрите на махалото (ω = √g / L, където г - ускоряване на тежестта, и L - дължината на проста махало (суспензия).
Уравнение малки трептения близо до равновесно положение (хармонична уравнение), както следва:
х + ω2 грях х = 0
Колебателно движение на махалото
Pendulum, което прави малки колебания, движещи синусоида. На второ място, за диференциално уравнение отговаря на всички изисквания и параметри на такова движение. За определяне на пътя, който трябва да зададете скоростта и координатите, които по-късно определят независими константи:
X = A грях (θ0 + ωt),
където θ0 - начална фаза, А - амплитуда на колебание, ω - цикличен честота, определена от уравненията на движение.
Махало (формула за големи амплитуди)
Тази механична система, изпълняват своите колебания с голяма амплитуда, то е предмет на по-сложни закони за движение. те се изчисляват по формулата за такива махало:
грях х / 2 = ф * зп (ωt / ф),
където SN - задължително Якоби, който за теб <1 является периодической функцией, а при малых u он совпадает с простым тригонометрическим синусом. Значение u определяют следующим выражением:
ф = (ε + ω2) / 2ω2,
където ε = E / СО2 (СО2 - енергия на махалото).
Определяне на нелинейни трептения период на махалото по следната формула:
където ω = π / 2 * ω / 2К (ф), К - елипсовидна неразделна, π - 3,14.
на махалото движението на separatrix
Той призова separatrix траектория на динамична система, в която двумерен фаза пространство един. Махалото се движи в неработен периодично. В безкрайно далеч точка на време тя пада от горното крайно положение към нулева скорост, а след това постепенно се набира. В крайна сметка той се спря и се върна към първоначалната си позиция.
Ако амплитудата на колебание на махалото се доближава до броя П. това предполага, че движението в равнината фаза е в близост до separatrix. В този случай, под действието на малък периодичен движеща сила на механичната система показва хаотично поведение.
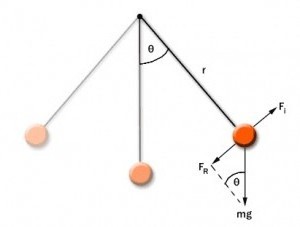
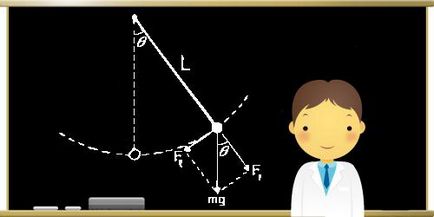
В случай на обикновено махало от равновесното положение с ср ъгъл настъпва тангенциална сила Fτ = тежестта -Mg грях φ. "Минус" знак означава, че тангенциален компонент насочена в обратна посока на посоката на отклонение на махалото. Когато се говори чрез махало изместване х протежение на кръгова дъга с радиус L е равна на ъглово отместване φ = X / L. Вторият закон на Isaaka Nyutona, предназначени за прожектиране на вектора на ускорение и силата получаване на желаната стойност:
мг τ = Fτ = -Mg грях х / L
Въз основа на това съотношение, ясно е, че на махалото е нелинейна система, като сила, която се стреми да се върне в своето равновесно положение, не винаги е пропорционална на х изместване, грях х / L.
Само когато математическата махалото извършва малки вибрации, той е хармоничен осцилатор. С други думи, тя се превръща в механична система в състояние да извършва хармонични трептения. Това сближаване е валидна за почти ъгли 15-20 °. Pendulum с големи амплитуди не е хармоничен.
закон на Нютон за малките колебания на махалото

Ако механичната система изпълнява малки колебания, закон на Нютон второто ще изглежда така:
мг τ = Fτ = -m * г / л * х.
Въз основа на това, можем да заключим, че тангенциалното ускорение на прост махало е пропорционална на неговото преместване със знака "минус". Това е състояние, при което системата се превръща в хармоничен осцилатор. Модул фактор пропорционалност между системите за изместване и ускорението е равно на квадрата на ъгловата честота:
ω02 = г / л; ω0 = √ г / L.
Тази формула отразява естествената честота на малките трептения на този тип махало. Въз основа на това,
Т = 2π / ω0 = 2π√ г / L.
Изчисления въз основа на закона за запазване на енергията
Имоти колебания движения махало могат да бъдат описани с помощта на закона за запазване на енергията. Трябва да се има предвид, че потенциалната енергия на махалото в гравитационно поле е:
Е = mgΔh = MGL (1 - защото α) = mgL2sin2 α / 2
Общата механична енергия е равна на кинетичната и максимален потенциал: Epmax = Ekmsx = E
След като сте написали закона за запазване на енергията, като производна на лявата и дясната страна на уравнението:
Тъй като производно на константите е равно на 0, тогава (ЕР + Ek) '= 0. производно на сумата е равна на сумата от производни:
Ep '= (мг / л * х2 / 2)' = мг / 2L * 2х * х '= мг / л * V + Ek' = (MV2 / 2) = m / 2 (V2) '= m / 2 * 2v * V '= MV * α,
Mg / L * XV + MVA = V (мг / л * х + m α) = 0.
Въз основа на последната формула, ние откриваме: α = - г / л * х.
Практическо приложение на математическата махалото
Гравитационно ускорение варира с ширина, тъй като плътността на кората около планетата не са идентични. Къде скали се срещат с по-висока плътност, тя ще бъде малко по-висока. Ускорение на математически махало често се използва за проучване. В помощ си вид за различни минерали. Просто отчитане на броя на трептения на махалото, е възможно да се открие на въглищата или рудата в недрата на Земята. Това се дължи на факта, че тези ресурси имат плътност и тегло повече от притайват хлабави скалите.
Математически махало, използван от такива видни учени като Сократ, Аристотел, Платон, Плутарх, Архимед. Много от тях смятат, че механичната система може да повлияе на съдбата и живота. Архимед използва математически махалото със своите изчисления. В днешно време, много окултисти и медиуми използват тази механична система за изпълнението на нейните пророчества, или търсенето на изчезнали хора.
Известният френски астроном и учен, Фламарион за техните изследвания също използва математически махало. Той твърди, че с негова помощ той е в състояние да прогнозира откриването на нова планета, появата на метеорита Тунгуска, и други важни събития. По време на Втората световна война в Германия (Берлин) работи като специализиран институт на махалото. В днешно време, тези изследвания не е на разположение в Мюнхен институт по парапсихология. Неговата работа с махалото, персоналът на тази институция, наречена "radiesteziey".
