Намерете лицето на успоредника построена на векторите
Asix Admin. Отговорих преди 4 месеца
Площта на успоредник. който е построен на векторите. Тя може да се намери като продукт на дължините на тези вектори и синуса на ъгъла между тях
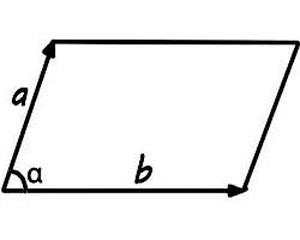
Ако в проблема определя дължината на тези вектори, намерете областта е лесна задача.
Ако не е посочен дължината на вектора, те трябва да бъдат намерени с помощта на координатите на тези вектори.
Вземем примера на изчисляване площта на успоредник вектори.
Пример 1.
Виж областта на успоредник, образуван от вектори, а на + 3b и 3а + B. Известно е, че дължината на вектори А и В са равни на единство, а ъгълът между тях е 30 градуса.
Решение.
Ние считаме, продукт на два вектора, който е построен на успоредник:
(А + 3b) (3a + б) = 3а * A + A * б + 9а * б + 3b * б.
Що се отнася до продукта на векторите на * и б * б или равни на 0, можем да запишем:
3а * A + A * б + 9а * б + 3b * б = 0 * 3 + A * б + 9Ь * а + 3 * 0 = A * б - 9а * б = -8а * б.
Намерете лицето на успоредник:
Отговор. Площта на успоредник е равна на 4.
Ако векторът е определена от нейните координати, първо трябва да се намери дължината им, посредством формула, според която дължината на вектора е равен на корен квадратен от сумата на квадратите на координатите.
Например, ако координатите на вектора са равни (7, 11, 17), неговата дължина ще бъдат открити по формулата: