Площта на успоредник, образуван от векторите - формула, примери от изчисленията

Предишен ◈ Следващото

Площта на успоредник, образуван от векторите е равна на произведението от дължината на тези вектори в ъгъл ъгъл, който се намира между тях.

Площта на успоредник, образуван от векторите - формула, примери от изчисленията

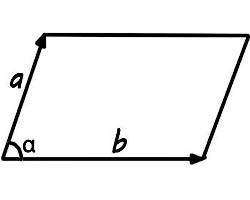
Е, когато условията са дадени на дължината на същите тези вектори. Въпреки това, също така се случва, че да се прилага формула областта на успоредник конструирана на векторите е възможно само след уреждане на координатите.

Ако имате късмет, а условията са носители на дължина, просто трябва да се прилага по формула, която сме разгледали подробно областта на успоредник в статията. Размер ще бъде равна на произведението на синуса на ъгъла между тях на модула:

Вземем примера на изчисляване площта на успоредника построена на векторите.

Цел: успоредник конструирана на векторите и. Търсене област, ако ъгълът между тях на 30 °.
Изразете вектор чрез техните стойности:

Може би имате въпрос - откъде нули? Струва си да припомним, че ние работим с вектори, и за тях. Също така имайте предвид, че ако в резултат получаваме израз, той ще бъде превърнат в. Сега ние извърши окончателното изчисление:

Нека се върнем към въпроса, когато векторите на дължина не са посочени в условията. Ако вашият успоредник се крие в Декартова координатна система, ще трябва да направите следното.

Изчисляване на дължини на страните на фигурите, дадени от координатите

За да намерите координатите на началната и крайната вектори координира изважда от съответните координати започват. Да предположим, че координатите на вектор (х1; y1; Z1) и вектор б (x3; Y3; z3).

Сега ние откриваме, дължината на всеки вектор. За тази цел всяка координатна да се изправи, след което се определят резултатите и от краен брой екстракт от корен. Според нашите изчисления вектори са следните:

Сега трябва да намерим нашия вътрешен продукт на вектори. За тази цел се добавят съответните координати и умножават.

С дължината на вектори и тяхното скаларно произведение, можем да намерим косинуса на ъгъла, разположена между тях.
Сега ние можем да намерим синуса на същия ъгъл:
Сега имаме всички необходими стойности, и ние можем лесно да се намери областта на успоредник изграден на векторите на вече известни формула.