Решения на уравнения (намиране на корените на уравнението), съдържание на платформа

Решения на уравнения (намиране на корените на уравнението)

Уравнение - равенство на два израза с променливи.

Решете уравнението -Find корените на това уравнение, или да докаже, че те не са.

1. Разширяване на скобите, ако има такива, се прилагат дистрибутивният имота

а (б + C) = а б + С

(А + В) (C + D) = С + с + д + б в б г

2. Корените на уравнението няма да се промени, ако има такива - термин, прехвърлени от една част от уравнението на друг, да се променя неговият знак.

(Казвайки променлива събират от едната страна на другата страна, както и промяна на знаци условията на номера, когато преминават през знака за равенство.) Пример:

3 (2 + 1,5 х) = 0,5 х + 24

6 + 4,5 х = 0,5 х + 24

4.5 х - = 0,5 х 24-6

Пример: изчисляване на координатите на точките на пресичане на линията 5 х 7 + у = 105 до координатните оси.

Решение: 1) за х-ос точка (21, 0)

у = 0; X 5 + 7 * 0 = 105 следователно х = 21

2) с ос OY точка (0; 15)

х = 0; 5 * 0 + 7 = 105 има тук у = 15

A: с точка на х-ос (21, 0) и DU ос точка (0; 15).

3. Корените на уравнението не се променят, ако двете части на уравнението за умножение или

разделена на един и същ номер не е равна на 0

Продуктът е равен на 0. Ако една от

0. фактори, които решаваме квадратното уравнение:

= 0 С теорема Wyeth имат

Def. Решаването на системата от уравнения с две променливи е двойка стойности на променливите, достъпни от всяка уравнение на системата в истинско равенство.

Методи за решаване на системи уравнения.

1) графики (графика изграждане на система от уравнения, ние получаваме координатите на графики пресечните точката на пресичане точки ще разтвори на уравнения).

изграждане на отделни редове 2 графики + 3Y = 5 и 3Y = - 9

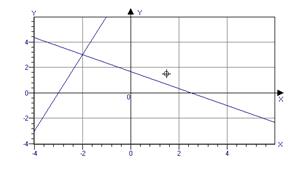
Ние се изгради графики на тези функции в една единствена координатна система и да намерят координатите на пресечните точки. В този пример, един пункт и неговите координати са х = - 2 и у = 3.

2) метод заместване (изразя една променлива през още една от уравнението за заместител на второто уравнение и решаване на полученото уравнение за една променлива, стойността намери заместител променлива във второто уравнение и да намерят втората променлива. И напишете отговор)

Пример. решаване на система от уравнения

- 5x 2 (7 - 3 х) = + 4Y) - 2у = 30

-5х 14 - 6x = 3 75 + 12у - 2у = 30

-11x = 3-14 10Y = 30-75

- 11x = - 11 10Y = - 25

х = 1, у = 7-3 = 4 * 1 Y = - 2.5 х = 25 + 4 * (- 2.5) = 15

Отговор. х = 1; у = 4 Отговор: х = 15; Y = - 2,5

3) Метод допълнение (размножават двете страни на първото уравнение на един номер. Двете страни на друга уравнението към друг номер, двете числа са такива, че те са получени чрез умножаване на идентични променливи с противоположни коефициенти)

Пример. решаване на система от уравнения

A: а = 10 б = 5

Пример: решаване на системата от уравнения

Отговор: х = - 10, у = 5

Пример: изчисляване на координатите на пресечните точки на линии

2 х - 3 и у = 7 + 5 х 4 у = 6

Решение: от състоянието на координатите на точки задоволи и двете уравнения, а след това има решения на тези уравнения на системата.

Директен у = к х + б преминава през точка А (- 1, 3) и В (2; Добави уравнение на тази линия.

Решение: директен заместител в уравнение координира стойностите, дадени точки и да получат уравненията на системата.

Пример: решаване на системата от уравнения

След това реши метод допълнение

Заместник в първото уравнение

Виж координатите на пресечните точки (-2, -1). (-2, 1). (2, 1). (2: 1)

Ето защо ние решим две системи от уравнения.

метод за допълнение GET Решаването: