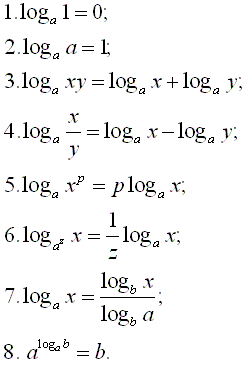Всички формули по математика
Тази страница съдържа всички формули, необходими за преминаване на теста и независими произведения, изпити по алгебра, геометрия, тригонометрия, твърди геометрия и други клонове на математиката.
Тук можете да изтеглите или да гледате онлайн всички основни тригонометрични формула, формула областта на окръжност, формулите на съкратена умножение формула обиколка, формули за намаляване и много други.
Можете също така да отпечатате необходимите колекциите на математически формули.
Академичен успех!
Аритметика Формула:
Алгебра формула:
Геометрични формули:
Аритметичната формула:
Закони операции на номера
Комутативен закон на добавяне: А + В = б + а.
Асоциативен право на прибавяне: (А + В) + с = а + (В + С).
Комутативен закон за размножаване: аб = ба.
Асоциативен закон за размножаване: (аб) а = а (бв).
Разпределителни право на умножение над допълнение: (А + В) с = променлив + бв.
Разпределителни право на умножение по отношение изваждане: (а - б) с = ав - ж.к..
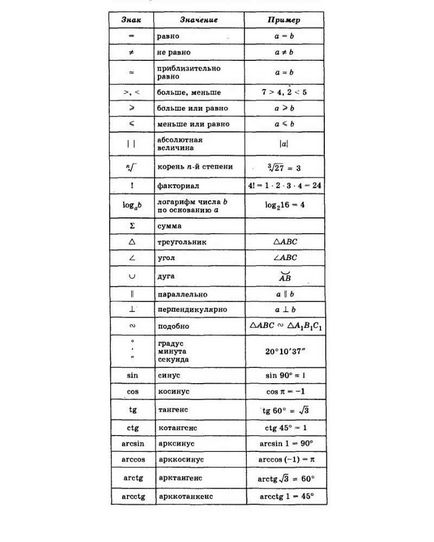
Някои математически символи и съкращения:
признаци на делимост
Признаци на делимост на "2"
Брой се дели на "2" безследно нарича дори. не се дели - странно. Броят е разделен с "2" без остатък, ако последната цифра chotnaya (2, 4, 6, 8) или нула
Признаци на делимост на "4"
Броят се дели на "4" без следа, ако последните две цифри от неговите или нули в сумата образуват число, кратно на "4"
Признаци на делимост на "8"
Броят е разделена от "8" без следа, ако последните три от неговите цифри нула или в размер образуват числата неделими от "8" (например: 1000 - последните три цифри "00", и като се раздели 1000 от 8 превръща 125 104 - последните две "12" се разделя на четири цифри и чрез разделяне на полученото 112 4 28; и т.н.)
Признаци на делимост на "3" и "9"
Без баланса на "3" се делят само тези числа, чиято сума от цифри се дели на "3"; на "9" - само тези, чиято сума от цифри се дели на "9"
Признаци на делимост на "5"
Без остатъка от "5" се разделя на броя на последната цифра "0" или "5"
Признаци на делимост на "25"
Не остатък на "25" се разделя на броя, последните две цифри от които са нула или в размер до образуване номера неделими от "25" (т.е., броят завършва в "00", "25", "50", "75 "
Признаци на делимост от "10", "100" и "1000"
Без баланса на "10" са разделени само броя, последната цифра е нула, за да "100" - само тези числа, в които през последните две цифри на нули на "1000" - само тези числа, в които през последните три цифри на нули
Признаци на делимост на "11"
Без баланса на "11" се делят само тези числа, чиято сума от цифри, заемащи странни места, или равен на сумата от числа, която заемат дори местата или се различава от това на броя неделими от "11"
Абсолютната стойност - формула (модул)
Формула Действия с фракции
Един формула инверсия в крайния знак рационално фракция:
Две равни отношения представляват част:
Основната част на имота
Намирането на дела на членовете
Пропорции. са еквивалентни пропорции. Производно част - следователно определен дял
Средните стойности
средна аритметична
Средната геометрична стойност (средна пропорционална)
средната квадратична
средно хармонично
Някои краен брой серия
Идентични трансформации алгебрични и тригонометрични изрази
свойства на правомощия
Имоти аритметични корени
За всяко положително число п и к, по-голямо от 1, и всеки неотрицателна А и В са верни равенство:полиноми
За всички, а, б, в и са истинско равенство:
Свойства на числовите неравенства
1) Ако 5) Ако
7) Ако (За греха на функции и COS - степента на понижаване на формула) (А1 - първият елемент; г - разлика п - брой членове; един - п-тия член; Sn - сумата от първите N условия): (В1 - първият елемент; р - знаменателя п - брой на членовете; милиарда - п-ти план; Sn - сумата от първите членове на N, S - сумата от безкраен прогресия Geom.): Ако функция F има производно в точка, оксо и функция г е производно на йо = F (оксо), комплекс функция H (х) = грам (е (х)) е производно на оксо, където: 1. Разстоянието между точките А1 (х1; Y1) и А2 (х2; y2) се получава от: 2. координатите (х; у) средата на краищата А1 (х1; Y1) и А2 (х2; y2) съхраняват от формули: 3. уравнение линия с наклон и пресечната има формата: Ъглов коефициент к е стойност на допирателната на ъгъла, образуван от права линия с положителната посока на оста Ox и отрязъкът р - стойност на ординатата на пресичане точка на правата линия с оста Oy. 4. Общото уравнение на права линия на форма: брадва + с + С = 0. 5. Уравнения на правите линии, успоредни съответно оси Oy и Ox, са от вида: 6. Условия за паралелни и перпендикулярни линии Y1 = KX1 + q1 и Y2 = kx2 + q2, съответно, са от вида: 7. уравнението на окръжност с радиус R и центриран при О, съответно, точките (0, 0) и С (оксо; йо) имат формата: Той представлява уравнение на парабола с връх в точката чиято абсциса 1. Разстоянието между точките А1 (х1; Y1; Z1) и А2 (х2; y2; z2) се получава от: 2. координатите (х; у, Z) с краищата на средния сегмент А1 (X1, Y1; Z1) и А2 (х2; Y2; z2) се дават от: 3. Модул вектор, определен от нейните координати, се изчислява по формулата: 4. При добавяне на вектори на съответните координати са оформени и чрез умножаване на вектора от редица всички координати се умножават по този номер, т.е. следните формули: 5. вектор единица е codirectional с вектора съгласно формулата: 6. скаларен продукт е броят: където - ъгълът между векторите. 7. точка продукта от два вектора 8. косинус на ъгъла между вектори и се получава от: 9. необходимо и достатъчно условие за перпендикулярни вектори и има формата: 10. Общото уравнение на равнина, перпендикулярна на вектора има формата: брадва + с + CZ + г = 0. 11. уравнение на равнина, перпендикулярна на вектора и минаваща през точка (оксо; йо; ZO), има формата: а (х - оксо) + б (у - йо) + C (Z - ZO) = 0. 12. уравнението на сфера с център О (0, 0, 0) се изписва като: 1) Броят на пермутации на п елементи се получава от: 2) Броят на подреждане на елементи на п т е с формула: 3) Броят на комбинации от п елементи на т се получава от: 4) следната комбинация от свойства: 5) Формула биномно има формата: Сумата на числата А и В е равно на п. 6) (к + 1) то термин се изчислява по формулата: 7) Броят на комбинации може да се намери на триъгълника на Паскал. Pascal триъгълник (до п = 7): 8) Количество на Биномен коефициент е равен до 2п. 9) За да намерите следващия член на биномно коефициент, е необходимо Биномен коефициент, умножен по предходния член на една фигура и да се делят на броя на предишните членове. Това е центъра на кръга - точката на пресичане midperpendiculars. Център на вписан кръг - в точката на пресичане на ъглополовящи. (А, В, С - страна - противоположни ъгли към тях; р - semiperimeter; R - радиус на окръжност кръга; R - радиусът на вписан кръг; S - площ; ха - височина внимание от страна на а): 2. правоъгълен триъгълник: Центърът на описаните окръжности съвпада с центъра на хипотенузата. (А, В - краката С - хипотенуза; ав, бв - проекция на краката на хипотенузата): 3. равностранен триъгълник: Медиана ъглополовяща. OR = Or. 4. произволна изпъкнал четиристранни (D1 и D2 - диагонал - ъгъл между тях; S - площ): (А и Б - съседни страни, - ъгълът между тях, ха - височина внимание от страна на а): Във всеки един диамант кръг може да се впише. Можете да опишете кръг около всеки правоъгълник. (А и Б - основа; Н - разстояние между тях; л - средната линия): 10. Описани многоъгълник (Р - semiperimeter; R - радиусът на вписан кръг): S = PR. 11. правилен многоъгълник (An - дясната п-гон; R - радиус на окръжност кръга; R - радиусът на вписан кръг): (R - радиус С - обиколка; S - площ на кръг): (L - дължина на дъгата, ограничаващ сектор, - степен мярката на централния ъгъл, - на радиан мярка на централния ъгъл): (L - страничен ръб; Р - периметъра на основата; S - отпечатък Н - височина; Psech - перпендикулярно на напречното сечение на периметъра; Sbok - странична повърхност; V - V): 2. Директно призма 3. кубовиден (А, В, С - размери; V - диагонал): 5. Произволен пирамида (S - отпечатък Н - височина; V - V): 6. Правилно пирамида (Р - периметъра на основата; л - Апотема; Sbok - странична повърхност): 7. произволно пресечена пирамида (S1 и S1 - квадратни основи; Н - височина; V - V): 8. Правилно пресечена пирамида (Р1 и Р2 - периметъра основи; л - Апотема; Sbok - странична повърхност): (R - радиус на основата Н - височина; Sbok - странична повърхност; V - V): (R - радиус на основата Н - височина; л - генератор; Sbok - странична повърхност; V - V): (R - радиус на сферата; S - площ на сферичната повърхност; V - V): (R - радиус на сферата; Н - височина сегмент; S - сферичен сегмент повърхност; V - V): (R - радиус на сферата; Н - височина сегмент; V - V):Отношенията между тригонометричните функции на същия аргумент
(Наричан записа п Je Z означава, че п - цяло число)
Присъединителните формули:
Формула на двойно аргумент:
Формула тройна аргумент:
Формула половина на аргумента:
Формула трето и четвърто степен:
Формула възлиза преобразуване в продукт:
Формула продукт превръщане в размер на:
формула редукция за превръщане на изразяване на Форма А) да се постави даден знак функция, която има оригинален функцията; б) функцията се променя на "kofunktsiyu", ако п е нечетен; функция не се променя, ако п е още. (Kofunktsiyami синус, косинус, допирателна и котангенс съответно нарича косинус, синус, и допирателна котангенс). Например:
ъгъл формула констатация:
Таблицата със стойностите
кръга на единица:
Формулата на напредък:
аритметична прогресия
геометрична прогресия
дериват
Основните правила на диференциация:
Производното на съставна функция:
Производни на тригонометрични функции:
Производното на логаритмичната функция:
Уравнението на допирателната към графиката на функцията: